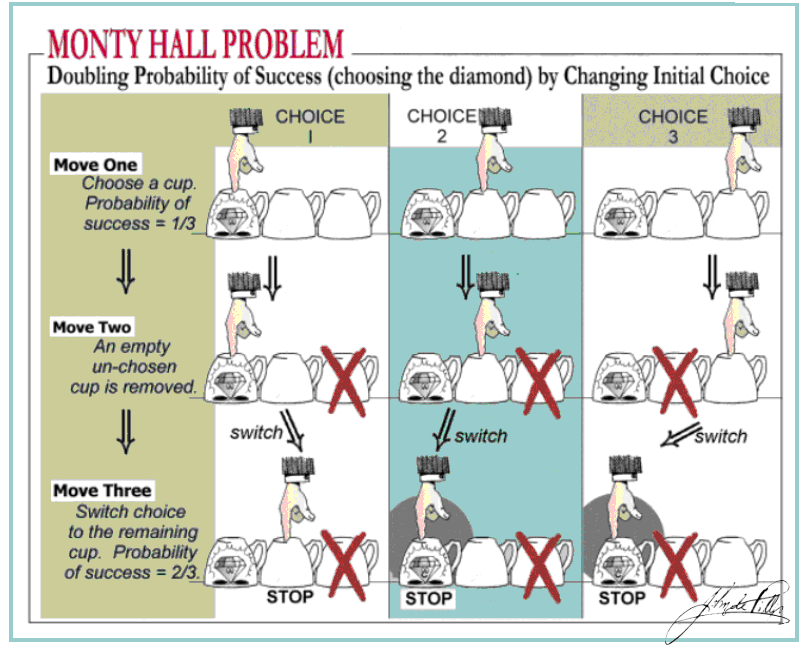
La importancia de tener un modelo para pensar sobre la realidad nunca debe ser desdeñada. De otra manera es difícil saber de qué estamos hablando. Véase, si no, esta entrada en el Otto Neurath o esta otra mía semanas atrás. Uno de los ejemplos más sencillos, a la vez que ilustrativo, es la paradoja de Monty Hall.Monty Hall es el presentador de un concurso televisivo. Una de las situaciones en las que se suelen ver inmerso el concursante es la siguiente. Debe elegir entre tres puertas, una de las cuales tiene tras ella un premio. Las otras dos no guardan nada. El concursante elige la puerta A y, a continuación Monty Hall abre una de las otras dos puertas, pongamos que sea la B, y se ve que no hay premio. Monty Hall le da la oportunidad al concursante de cambiar y elegir la C, si quiere. ¿Debe el concursante cambiar de puerta?
Esta es una vieja paradoja y no es mi intención elaborar sobre ella. Sólo la tomo de referencia para ilustrar la necesidad de los modelos. Tal como yo he descrito la historia, nos falta saber cómo se ha llegado a la situación descrita. En particular, es necesario saber si Monty Hall sabía dónde estaba el premio y si, sabiéndolo, deliberadamente escoge la puerta en que sabe que no está.
Si Monty Hall abre una puerta al azar y sucede que no hay premio, las probabilidades a priori de que el premio esté tras A o tras C siguen siendo iguales (el 1/3 de probabilidad de B se pasa a medias a A y a C, quedando en 1/2 cada una) y el concursante no gana nada por cambiar.
Si, en cambio, Monty Hall sabe dónde está el premio y abre una puerta donde sabe que no está, la probabilidad de 1/3 de B se va toda a C, de manera que al concursante le conviene cambiar.
El modelo lo es todo. Intentar responder a la cuestión sin especificar qué caso tenemos en mente solo nos puede llevar a un gran dolor de cabeza tras una larga discusión.
Aclaro dos cosas. La formulación original de la paradoja narraba el segundo escenario. Sin embargo, mucha gente pensaba que la solución seguía siendo 1/2 y que no hacía falta cambiar. No me molesto en hacer los cálculos y las explicaciones de cómo se llegan a estas conclusiones porque está en cualquier página dedicada al asunto, incluidas las entradas en la wikipedia y en la ilustración que abre esta entrada. Pinchad sobre ella para verla completa.
Este problema (que también se conoce como paradoja de las tres puertas) fue el que me enganchó definitivamente al estudio y el coqueteo con la probabilidad. Y soy incapaz de salir.
ResponderEliminarExcelente entrada y blog, ya habia leido esta paradoja vista de otra manera, te invito a mirarla en el blog eltamiz.com
ResponderEliminar¡Que gran título!
ResponderEliminarA propósito, yo leí esa historia en una novela. Al parecer la solución correcta fue propuesta por una superdotada y fue criticada por eminentes matemáticos. Increíble, ¿verdad?
Hector1564:
ResponderEliminarHablas de Marilyn vos Savant.
Sí, y del libro El curioso incidente del perro a medianoche.
ResponderEliminarEugenio:
ResponderEliminarDesde luego, esta es una de las paradojas más famosas de la probabilidad y engancha a cualquiera. Según creo, la formulación de Marilyn vos Savant podía dar lugar a ambas interpretaciones (corrígeme si me equivoco), aunque, en su solución, Marilyn dejaba claro cuál era su modelo.
Namtaru:
Bienvenido al blog, y gracias por el piropo. A ver qué discos nos seleccionas en el tuyo. Estaré atento.
Héctor:
Gracias por la referencia. No me acordaba que en "El curioso incidente..." se hiciera referencia a la paradoja. ¡Está en tantos sitios!
Todos:
Tengo pensado hacer más entradas sobre paradojas, algunas poco conocidas. Esas las explicaré con más calma. Para todas servirá haber recordado la de Monty Hall (o de las tres puertas, como bien dice Eugenio).
Imaginemos que como científico me planteo 'pensar la realidad'.
ResponderEliminarSi pensar quiere decir algo parecido a 'predecir' (anticipar el mundo, para comprenderlo y, en su caso, cambiarlo), y no en resolver analíticamente un problema matemático (o estadístico): ¿qué debería hacer para predecir el comportamiento (la decisión, la interpretación) de una muestra aleatoria de la población mundial enfrentada al 'Monty Hall problem'?
Dicho de otra manera, sé que necesito un modelo como marco de referencia. Pero, ¿necesito algo más?
Hank:
ResponderEliminarDeberías coger una muestra aleatoria de la población mundial (se hace un podo difícil, ¿no te conformas con una de un país?) y ponerlos a elegir en una simulación del problema, con algún premio monetario (10 euros serían más que suficientes), para que tengan incentivos a pensárselo. Estas cosas se hacen en economía experimental todo el tiempo, pero no me consta que hayan experimentado con este ejemplo.
Tal vez quieras hacer varias versiones del caso. Una en la que deje claro que el presentador elige al azar, otra en la que elige la puerta que sabe que no tiene premio y otra en la que la cosa quede un poco ambigua.
Así puedes saber si atienden o no al modelo explícito y qué pueden estar pensando cuando no se les da el modelo.
Creo que el problema se formula, teniendo en cuenta que Hall conoce dónde se oculta el premio. Se trata de un problema que uso con mis alumnos en una práctica de pensamiento formal, y que muy pocos resuelven correctamente. Aunque supuestamente dominamos el esquema formal de probabilidad, cuando, como en este caso, se complica algo la formulación del problema, muy pocos los resuelven. Tengo que reconocer que a mí me costó trabajo.
ResponderEliminarUn saludo
Hola Alfredo, me alegra tenerte por aquí.
ResponderEliminarEfectivamente, nuestra mente no tiene una clara intuición de las probabilidades, como pueda tenerla, por ejemplo, de las distancias en nuestro entorno. Menos aún cuando la cosa se complica con la regla de Bayes. Por eso, aunque la podamos aprender "en teoría", a la hora de aplicarla, exige mucha práctica, y aún así siempre caemos en alguna.
Saludos.
Efectivamente los modelos son importantisimos, a mi me dio por debatir sobre esta paradoja con mis amigos un viernes por la noche, y al final la única manera de convencerles del razonamiento correcto fue con vasos y monedas... cuando hay un cabezota cerca, a veces mejor que las palabras es algo con lo que darle en toda la cabezota.
ResponderEliminarY por cierto, perdon por entrar sin llamar ni presentarme primero.
Hola, Maskuko.
ResponderEliminarNo hay que pedir perdón. Aquí todo el mundo es bienvenido. En cuanto al convencimiento experimental, también lo he probado y es estupendo. Para que se vea que las matemáticas también son empíricas.
Un saludo.
No puedo corregirte o darte la razón porque el asunto de Marilyn lo estudié hace mucho tiempo. Es hora de darle un repaso, y lo haré. Además, estoy preparando una minientrada sobre explicando la paradoja a mis alumnos, a ver si me sale.
ResponderEliminarEugenio:
ResponderEliminarTe recomiendo el tratamiento experimental (tal vez después de la explicación que encuentres más convincente) como sugería Maskuko. Es realmente iluminador.